Causal Sets

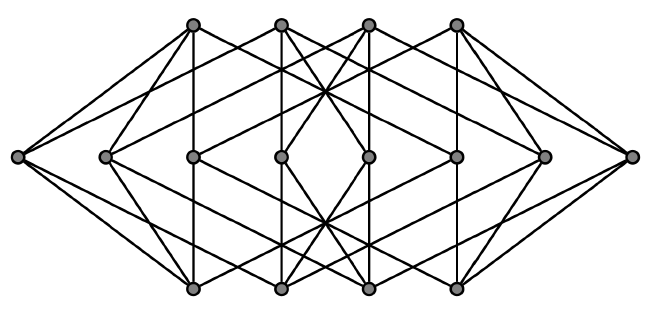
Kleitman-Rothschild Sets #

My published work deals with causal set theory, a proposal for the quantization of space-time. If you randomly sprinkle a large number of points in space and time, you can reconstruct important features of the space-time manifold just from the causal connections between the points (i.e., which points are close enough in space or far enough in time to influence each other, given imformation moving at the speed of light). The problem with this picture is that for this procedure to reliably work you need to start with space and time, the very things you’re trying to argue are not fundemental. If you instead start with a random distribution of causal links, instead of looking like a manifold, it will almost always form some small number of moments of time (typically three, an arrangement known as a Kleitman-Rothschild order).

This distribution of causal sets presents a problem, as the natural way to work with quantum gravity on these sets is a path integral across all possible arrangements. In Path Integral Suppression of Badly Behaved Causal Sets, my collaborators and I show that Kleitman-Rothschild sets, while common, have a negligible impact on the path integral, as the weight given by each due to its action drops as \(2^{-n^2}\). Our followup work, The Einstein–Hilbert action for entropically dominant causal sets, extends this result to other such layered sets.

The main body of the work, and my primary contribution to it, consists of combinatorics. The formula used for the action involves counting the number of points in 2 layers that are connected through exactly some small number of intermediate points. As it is highly unlikely that there are no other intermediate points, the number of such arrangements in any given set falls extremely quickly with the set’s size.